Лабораторна робота
Тема: Застосування обчислювальних можливостей MathCAD
Мета:Отримати навички застосування обчислювальних можливостей MathCAD під час вирішення професійних завдань
Література Л-5, Л-10, Л-11.
Теоретичні відомості
Математична програма MathCAD надає вже звичні, потужні, зручні та наочні засоби опису алгоритмів, розв'язання математичних задач. Система має достатні можливості для виконання найбільш масових символьних (аналітичних) обчислень і перетворень. Більше 600000 тільки зареєстрованих користувачів володіють різними версіями системи MathCAD у всьому світі, а з випуском нових версій системи це число значно збільшиться. Про систему з такою обчислювальною потужністю, як MathCAD, ще пару десятків років тому не могли мріяти навіть розробники унікальної наукової та космічної апаратури. Але ця потужність аж ніяк не утруднює на диво просте та інтуїтивно передбачуване спілкування з системою на загальновизнаній мові математичних формул і графіків.
Для вирішення кількох рівнянь сумісно MathCAD надає блок рішень. Блок рішень складається з групи рівнянь і нерівностей та закінчується функцією Find чи Minerr.
Блок рішень складається з наступних частин:
■ Блок розпочинається з ключового слова Given;
■ Тіло блоку складають рівняння - звичайні визначення та обмеження. Обмеження (constraints) - це рівняння чи нерівності, які MathCAD буде намагатися розв'язати. Блок необмежений по горизонталі. Будь-яке рівняння, яке написане нижче заголовка блоку і розташоване вище кінця блоку, є таким, що знаходиться в блоці.
■ Блок завершується одною з функцій Find(variable1, variable2, ...) або Minerr(variable1, variable2, ...). Аргументи в даних функціях задають змінні, які треба знайти. Функція Find повертає наступні значення: якщо функція має тільки один аргумент, то повертає значення тієї змінної, яка розв'язує обмеження. Якщо функція має кілька аргументів, то повертає вектор відповідей: одне значення для кожної змінної, загалом цей вектор розв'язує обмеження. Функція Minerr подібна Find, але повертає значення, які мінімізують похибки в обмеженнях, замість їх розв'язання.
Змінні, які використовуються як аргументи, попередньо повинні бути визначені на початку блоку рішень. MathCAD використовує ці значення як початкові.
Обмеження, що складають тіло блоку рішень, на відміну від звичайних рівнянь MathCAD можуть мати вирази з двох сторін знака "дорівнює". Обмеження мають дві форми: рівності та нерівності. Синтаксис першої форми expression1 = expressіon2.
Для розв'язання цього рівняння MathCAD намагається знайти значення змінних, які роблять два боки рівними один одному. Форма нерівності має замість знака "дорівнює" наступні знаки: >, <, <=, >=. Процесор намагається знайти значення змінних, які роблять вірним задане відношення.
MathCAD розв'язує обмеження, які містять тільки скалярні змінні.
При створенні блоку рішень треба перевести MathCAD у ручний режим обчислень, що попередить спроби знайти розв'язок незавершеного блоку рішень.
Математичний процесор розв'язує блок рішень методом ітерацій з початковими значеннями, що задані раніше. Якщо початкове значення дійсне, то буде відшуковуватися дійсне рішення, а якщо комплексне, то комплексне рішення. Проміжні результати не виводяться на екран, виводиться тільки кінцевий результат. Для кожного обмеження MathCAD визначає константу похибок, за якою визначається як далеко до вірного значення. Всі ці значення похибок визначають вектор похибок, який недоступний користувачеві, але грає важливу роль при виконанні ітерацій. На кожному кроці обчислюються нові значення змінних, які зменшують величину похибок для обмежень. Обмеження є вирішеними, якщо похибки становлять менше ніж величина TOL. TOL — це внутрішня змінна зі значенням по замовчуванню 0,001. Значення TOL можна змінити для підвищення точності обчислень. MathCAD повертає тільки одне рішення обмежень. Для знаходження інших рішень необхідно використовувати інші початкові умови. Іноді попередньо обмеження розв'язують графічно, а потім тільки за допомогою блоку рішень.
Блок рішень із функцією Find завершує свою роботу в наступних випадках:
■ знайдено рішення;
■ рішення не знайдено і немає подальших поліпшень проміжних результатів;
■ MathCAD не може продовжувати далі обчислення, тому що виконано занадто багато ітерацій без помітного наближення до результату;
■ задано занадто багато обмежень.
По закінченні блоку рішень змінна ERR містить величину вектора помилок (суму квадратів усіх елементів вектора помилок). Значення, що видає функція Find, можуть використовуватись у наступних обчисленнях.
Функція Minerr завжди видає результат. Часто (але не завжди) він мінімізує похибки в обмеженнях.
Однією з найбільш корисних рис MathCAD є можливість визначення функцій користувача, які будуть розв'язувати обмеження. Якщо визначити функцію користувача в термінах функції Find, то нова функція буде розв'язувати рівняння та нерівності в блоці рішень кожен раз, коли вона буде використовуватись. Для визначення функції користувача в термінах функції Find необхідно блок рішень завершити наступним чином:
f unc(fvars):=find(varl, var2,...)
У цьому визначенні:
func - ім'я функції;
fvars - список змінних, що входять до обмежень. Цей список може містити аргументи функції Find або інші змінні. Якщо будь-яка зі змінних Var 1 , Var2 ... не з'являється в цьому списку, то MathCAD використовує початкові значення для неї, що задані вище Given блоку рішень.
Var1, Var2 - змінні, які повинні бути розв'язані в Find.
Результатом є значення (або вектор значень), яке розв'язує обмеження, використовуючи величини, що задані змінними fvars.
MathCAD може обчислити похідну, повертаючи оцінку похідної в точці. Результат обчислення похідної не функція, а скалярне число. Вираз, для якого обчислюється похідна, може бути дійсного або комплексного типу. Точність обчислень залежить від значення змінної TOL.
Алгоритм чисельного диференціювання робить послідовні наближення до значення похідної і зупиняється, коли наближене відрізняється від значення похідної на величину менше TOL.
MathCAD може показати і вичислити певні інтеграли. Щоб створити знак інтеграла введіть "&". Межі інтегрування повинні бути дійсного типу. Вираз під інтегралом може бути дійсного і комплексного типу. Всі змінні в інтегралі повинні бути визначені (за виключенням інтегральної змінної). Інтегральна змінна повинна бути одиночною змінною. Точність обчислення залежить від значення внутрішньої змінної TOL.
Програма може обчислити складні контурні інтеграли. Спочатку потрібно параметризувати контур, потім інтегрувати по параметру.
MathCAD може обчислити подвійні множинні інтеграли. Для завдання подвійного інтегралу після першого натискання на клавішу натисніть її ще раз. Однак обчислення подвійного інтеграла займає додатковий час, тому по можливості використовуйте еквівалентний одинарний інтеграл замість подвійного.
У процесор вбудовані функції, які дозволяють розв'язувати оптимізаційні задачі. Це функції minimize та maximize. Клацання правою кнопкою миші по імені "функції, що обчислює" (minimize, maximize, minerr, find) викликає додаткове меню зі списком трьох можливих методів чисельного рішення задачі (метод Левенберга - Маркворта, метод Ньютона та градієнтний метод) та їх деталі.
У MathCAD користувачу надана можливість вибору чисельного методу при рішенні інших задач. Так, наприклад, якщо клацнути правою кнопкою миші по оператору визначеного інтеграла, то з'являється список методів чисельного інтегрування.
Хід роботи
1. Самий простий спосіб знайти корінь рівняння з одним невідомим забезпечить функція root. Наприклад, необхідно знайти корінь рівняння x=cos(x). Слід задати початкове значення х:= 1 , рішення подається функцією
root(x - cos(x),x) =0.74
Точність обчислень задається системною змінною TOL, яка по замовчуванню рівна 10-3 і визначена в меню Math / Options (Математика / Параметры).
Проілюстру йте отримане рішення.
TOL:=10-3 x o :=root(x-cos(x),x).
хо=0.739, х=0,0.05. . 1
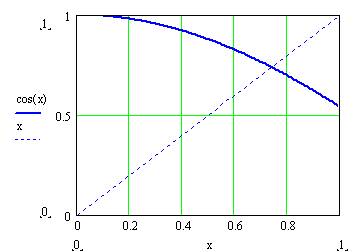
У цьому випадку змінено значення системної змінної TOL. Х0 - змінна із текстовим індексом, який вводиться за допомогою крапки: х.О. Текстовий індекс — це просто декоративна окраса, яка є складовою імені змінної.
Треба відмітити, що при виведенні результату відображається лише три знаки після десяткової крапки. Цю установку можна змінити в меню Format / Number у змінній Displayed Precision (Формат / Результат / Точность отображения).
2. Пошук коренів за допомогою блоку Given … Find(...)
Можна розв'язувати системи рівнянь із кількома змінними, однак, як і в попередньому випадку, необхідно задати початкові точки від яких буде відбуватися пошук рішення. Рішення шукається методом ітерацій, однак за наявності кількох коренів, очевидно, буде знайдено лише найближче рішення, якщо воно існує.
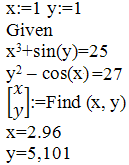
Таким же чином можна розв'язувати і системи лінійних рівнянь, однак треба задавати початкову ітерацію, тому системи лінійних рівнянь краще вирішувати матричним методом.
3. Пошук рішення за допомогою блоку Given … Minerr(...).
Практично те ж, що і в попередньому випадку, однак рішення буде знайдено в будь-якому випадку, навіть за його відсутності. Справа в тому, що слід шукати не рішення системи, а мінімальне значення рівнянь. Розглянути функцію, про яку заздалегідь відомо, що вона не має дійсних коренів, і знайти точку, в якій ця функція найбільш наближена до вісі x .
При побудові графіка необхідно вказати початкове значення

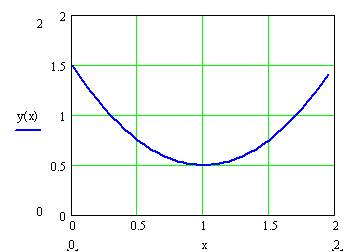
Для цього простого випадку очевидно, що найменші значення функції будуть при х=1.
х:=0
Given
у(х)=0
Minerr(х)=1
Перший рядок дає нам рішення х=1, а системна змінна ERR показує значення рівнянь.
ERR=0,5.
Аналогічно розв'язуються і більш складні рівняння чи їх системи.
4. Розв'язати систему рівнянь
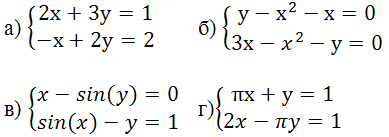
5. Розв'язати систему лінійних рівнянь двома способами:
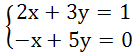
Матриці коефіцієнтів
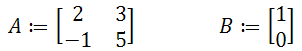
Система може бути подана як АХ =В.
Слід шу кати рішення матричним способом

І, нарешті, за допомогою блоку Given ... Find(...)
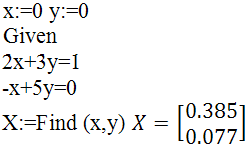
6. Розв'язання рівнянь у символьному вигляді.
Деякі рівняння MathCAD може розв'язати в символьному вигляді.
Для цього існують кілька можливостей:
ü записати квадратний трьохчлен, виділити змінну х і вибрати в меню пункт Symbolics / Variable / Solve (Символы / Переменные /Вычислить).
Отримаємо рішення в символьному вигляді.
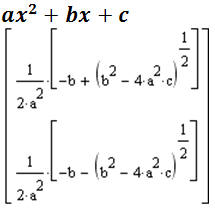
Для того, щоб рішення було записано справа від виразу, необхідно встановити прапорець Horizontally (Горизонтально) в меню Symbolics / Evaluation Style (Символы / Стиль Вычислений);
ü вирішити систему лінійних рівнянь
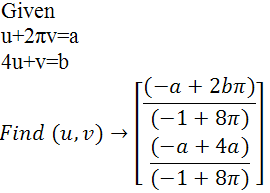
У цьому випадку необхідно вводити невикористані до цього часу змінні u, v, оскільки змінні х, у вже визначені. Обійти ці труднощі можна просто, якщо розв'язати рівняння на новому робочому листі.
7. Для обчислення сум і добутків скористатися палітрою обчислень.![]()
Обчислити
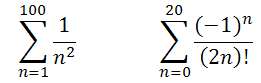
У цьому випадку використано знак суми з вказаними границями додавання. З прикладів видно, що система опрацьовує ситуації (-1)°=1, 0!=1
8. Знак додавання тільки з указанням індексу використовується для роботи з матрицями та функціями, що залежать від індексу, тобто в тих випадках, коли границі зміни індексу вказуються у вигляді змінної інтервального типу. Обчислити
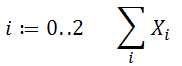
Необхідно створити свою матрицю X
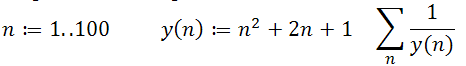
9. Аналогічно обчислюється добуток.
За визначенням
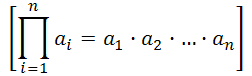
Обчисліть
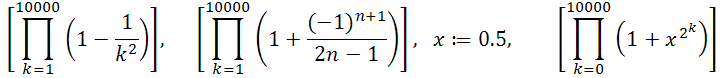
10. Обчислити для матриць М і D (їх задати довільно) суму та добуток діагональних елементів.
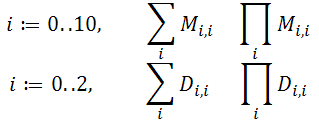
11. Обчислити інтеграли, якщо f(x): = x3– 3 ,1 х 2 +2,05х+1
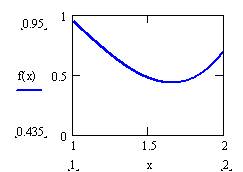
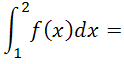
Визначений інтеграл - це площа криволінійної трапеції. Інтеграл достатньо легко обчислюється, якщо підінтегральна функція не має особливостей.
Точність обчислень задається системною змінною TOL, яка може бути задана в меню Math / Options.. (Математика / Параметры). Встановити, наприклад, 10-8.
12. Виконати символьні обчислення
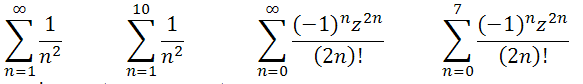
13. Аналогічно обчислити добуток
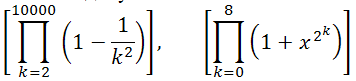
14. Обчислити первісні в символах f(x): =x sin(х2)
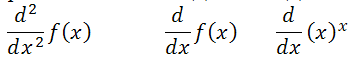
Для обчислення первісної достатньо поставити функцію під знак d Якщо перед цим визначити значення змінної, то отримаємо чисельне значення
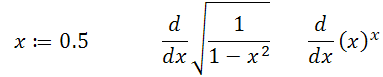
Перевірити
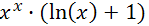
15. Транспортна задача: необхідно щоденно з першого складу перевозити до двох магазинів 50 телевізорів, а з другого складу - 70. При цьому перший магазин продає за добу 40 телевізорів, а другий -80. Відомі витрати на перевезення телевізорів зі складів до магазинів: 1200 у. о. - при перевезенні одного телевізора з першого складу до першого магазину, 1600 - з першого складу до другого магазину, 800 -з другого складу до першого магазину та 1000 - з другого складу до другого магазину. Як потрібно організувати перевезення, щоб витрати були мінімальними.
Ввести позначення:
х1 - кількість телевізорів, що перевозять із першого складу до першого магазину,
х2 - з першого складу до другого магазину,
х3 - з другого складу до першого магазину,
х4 - з другого складу до другого магазину.
Цільова функція має вигляд
f(x 1 ,x2,x3,x4):=1200x 1 +1600x2+800x3+1000x4
її треба мінімізувати. Перше наближення
х1:=0 х2:=0 х3:=0 х4:=0,
Обмеження
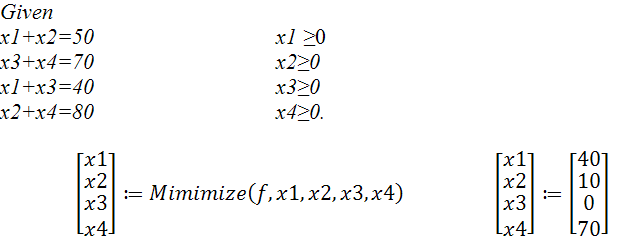
Проаналізувати результат
f(xl,x2,x3,x4)=134000.
Відповідь: мінімальні витрати на перевезення - 134000 у. о.
Питання для самоперевірки
1. Яка повинна бути кількість аргументів функції "Find" при вирішенні системи рівнянь?
2. За допомогою яких функцій можна розв'язувати задачі оптимізації?
3. Як працює функція Minerr?
4. Які форми мають обмеження, що складають тіло блоку рішень?
5. За допомогою яких клавіш у MathCAD вводиться знак "дорівнює"?
6. В яких випадках блок рішень із функцією Find завершує свою роботу?
7. Що означає вбудована змінна ERR?
8. Як задати функцію користувача?
9. Який знак введе в документ символ "&"?
10. Для чого використовуються функції Minimize та Maximize?